Basically, probability is concerned with ignorance. Probability can be discussed quantitatively because even about ignorance, exact statements can be made. Although we do not know in advance the result of the toss of a coin, we do know that the probability of heads is 0.5. Insurance companies, ignorant of the fate of any policyholder, can nevertheless set premiums intelligently. A gambling casino, ignorant of the outcome of any game, can nevertheless adjust odds to assure a profit. A physicist, ignorant of the lifetime of any particular muon, can nevertheless predict accurately the average lifetime of a collection of muons, and predict the exponential decay of the aggregate. In an experimental measurement, the thing we are ignorant of is the magnitude of the error. By chance a particular measurement might be precisely correct. Or it might have a significant error. In order to make a meaningful comparison between experiment and theory, the physicist must be able to assess the probable magnitude of the error.
Suppose a college catalogue states that the area of a single student’s room is 160 ft2, and a student decides to check this number. She measures the length of the room and its breadth and multiplies these two numbers together to obtain, perhaps, 156 ft2. Has she demonstrated that the college catalogue is wrong? Not necessarily. It depends on the uncertainty of her measurements. Determination of the uncertainty is usually not easy, and may amount to little more than an educated guess. She might guess, for instance, that her length and breadth measurements are accurate to within about 2%. This would imply that her area determination should be accurate to within 4%. She would then write down for her experimentally determined area,
(156 ± 6) ft2,
indicating her opinion that the true area probably lies somewhere between 150 ft2 and 162 ft2. Therefore her measurement would be consistent with “theory,” as set forth in the catalogue.
A somewhat better, but still not foolproof, way to determine uncertainty is by repeated measurement. If several measurements of the area of the room agree to within 6 ft2, the student can be more confident that the correct value lies within 6 ft2 of her first measurement. However, repeated measurement reveals only random error. Another kind of error, called systematic error, could result from a defective ruler or a consistently faulty measuring technique. These sources of error would act always in the same direction rather than randomly in both directions. Having assessed all sources of error, the physicist tries to assign an uncertainty defined as follows: It should bracket a range of values within which the correct value has a 66% chance to lie, and outside of which the correct value has a 34% chance to lie. Thus, if it had been possible to define the uncertainty with this much certitude for the room area measurement, the expression (156 ± 6) ft2 would mean that with a probability of 0.66, the true area has a value between 150 ft2 and 162 ft2, but with a probability of 0.34, might be less than 150 ft2 or greater than 162 ft2.
For only one kind of error, called statistical error, is it actually possible to determine the uncertainty of a measurement accurately. Statistical error results from the measurement of purely random events. It might be determined, for example, that in a particular radioactive sample, exactly 100 nuclei decay in a one-minute interval. In one sense, this measurement is completely free of error, for we may suppose that the number 100 was determined with complete precision. In another sense, however, it does have “error,” for it may differ from the average number of decays in other identical samples. The quantity of real physical importance is the average number of decays per minute in a large number of identical samples. It is this average rather than the actual number of decays for a particular sample that can meaningfully be compared with theory. Thus the idea of error enters in seeking an answer to the question: By how much is the average number of decays for all such samples likely to differ from the actual number measured for this sample? With this understanding of what is meant by the “error” of a precise measurement, a very simple answer to the question can be given. The uncertainty (a better term than “error”) associated with the measurement of n random events is √n. If a particular radioactive sample undergoes n decays in a given time interval, the average number for all such samples can be said to be equal to
n ± √n.
That is, the correct average has a 66% chance to lie within the range n – √n to n + √n. If one student in a laboratory measures 100 decays in a minute, he predicts that the average number measured by all of the students working with identical samples will be 100 ± 10. There is a good chance (probability two-thirds) that the true average lies between 90 and 110. This also means that about two-thirds of the students should record values within this range.
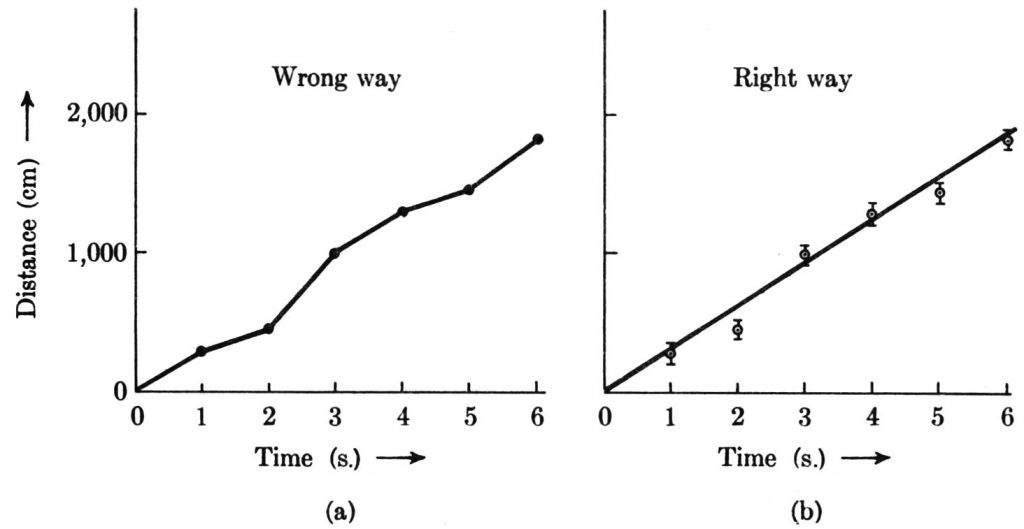
My discussion to this point has concerned experimental errors associated with single measurements. Experimental error also plays a very important role in the determination of functional relationships. A curve cannot sensibly be drawn precisely through each experimentally determined point in a graph, for the experimental errors in the measurements are reflected in an uncertainty of location of the points in the graph. Suppose that we wish to determine the functional relationship implied by the following set of time and distance data for a moving object.
| Time (s) | Distance (cm) |
|---|---|
| 1 | 280 |
| 2 | 450 |
| 3 | 1,000 |
| 4 | 1,300 |
| 5 | 1,450 |
| 6 | 1,840 |
Suppose further, for the sake of illustration, that the time measurements are so precise that their errors can be ignored and that the distance measurements are rather crude, with the uncertainty of each estimated to be ±70 cm. The figure below shows the wrong way and the right way to handle these data graphically. In the wrong way, the measured values are simply joined by straight-line segments. This is wrong first because the experimental errors mean that the plotted points need not represent the actual position of the object; second because the data provide no evidence about exactly how the motion occurred between the times of measurement. In the right way, the uncertainties are incorporated into the graph by attaching to each data point an error line extending 70 cm above and 70 cm below the point. These lines at once provide a picture of where the object most probably was at each time. Next a smooth line or curve is drawn among the points with no more details of shape and curvature than is justified by the magnitude of the uncertainties. In this example, a straight line adequately fits the data, and it would not be justifiable to seek a “better” fit with a curve. This, of course, does not mean that the straight line necessarily represents the actual motion accurately. We can say only that within the accuracy of the measurements, it is consistent to make the simplest assumption, namely, that the motion occurred with uniform speed such that the distance vs. time graph is a straight line. If the uncertainty of ±70 cm indeed spans a range of values containing the correct distance value with 66% probability, the line drawn among the points should cut through approximately two-thirds of the error lines and miss one-third of them. The fact that the straight line in graph (b) cuts four error lines and misses two tends to support the assumption that the straight line provides an adequate representation of the data. The slope of the straight line then provides a value for the speed of the object. In the figure, the slope of the line is 300 cm/s. It is a nice problem to estimate the uncertainty of this speed determination.