In connection with his original suggestion that energy transfer from matter to radiation is quantized, Max Planck introduced a numerical constant, now known as Planck’s constant, for which the usual symbol is h. Its value is h = 6.6261 × 10–34 kg m2/s (or joule second, J s). The dimension of h is the same as the dimension of angular momentum (mass × distance × speed), which in turn is the same as the dimension of energy × time. Planck’s constant has turned out to be the fundamental constant of quantum mechanics, in much the same way that the speed of light is the fundamental constant of relativity. It is obviously, by macroscopic standards, an extremely small quantity. In the domain where it rules, it is neither small nor unimportant. Planck’s constant determines the entire scale of the submicroscopic world—the energy of photons, the spin of particles, and the size of atoms.
Albert Einstein related the constant h to the energy carried by electromagnetic radiation. I discuss the particle of light—the photon—in Essay Q9. Niels Bohr and John Nicholson were among the first to see a wider significance of Planck’s constant as the basis of a general quantum principle in nature. Both recognized angular momentum as a granular variable. In 1915 William Wilson and Arnold Sommerfeld independently gave the general rule for angular-momentum quantization,
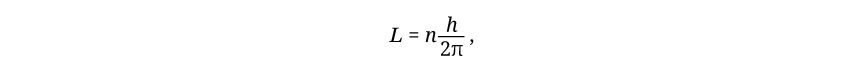in which L is angular momentum and n is any integer. The combination h/2π has proved to be so ubiquitous in quantum theory that it deserves its own symbol, ħ (pronounced “h-bar”). Its numerical value is
ħ = 1.05457 × 10–34 J s.
Thus ħ is the quantum unit of angular momentum in nature. The discovery by George Uhlenbeck and Samuel Goudsmit in 1925 that the electron has a spin angular momentum equal to 1⁄2ħ upset the Sommerfeld-Wilson rule somewhat, but it proved to be possible to incorporate this discovery into quantum mechanics without difficulty. We understand now that particle spin may be either an integral or a half-integral multiple of ħ, although orbital angular momentum is restricted, as Nicholson and Bohr first guessed, to integral multiples of ħ.
Not all of nature’s granularity is understood. The reasons for discontinuity of energy and of spin are provided by quantum theory. But why mass and charge come only in lumps of certain sizes remains a mystery and a challenge. Perhaps a new quantum constant, analogous to Planck’s constant, is waiting to be discovered.