The concept of a particle, however small it may be, is easy to grasp. You can picture a golf ball and imagine it shrunk down to fundamental-particle size, about 10–15 m. You see in your mind’s eye a tiny spherical lump of matter. It has mass; it is located at some definite point; it can move from one place to another at some measurable speed. Energy is required to set it in motion, and it gives up energy when it is slowed down or stopped. Picturing a massless particle that always shoots about at the speed of light is a bit harder (but it can be done). Here I shall stick to more conventional material particles to illustrate what is called the wave-particle duality. At first thought, waves seem to be different from particles in every way. A particle has mass, can be located at a definite point, and can be imagined to have a definite size; a wave is massless, is necessarily spread out, and has an ill-defined size. Moreover, the quantities used to characterize a wave—its amplitude, wavelength, and frequency—are quantities that seem to have no meaning for particles.
In spite of these obvious differences, quantum mechanics has succeeded in merging the ideas of waves and particles. To make the merger reasonable, let us consider those properties that waves and particles do have in common, even in our macroscopic world. First of all, both obviously can travel from one place to another, and at a definite speed. But here, too, there is a difference. The speed of a wave usually depends very little on its wavelength or its amplitude. Fortunately for the listener at the back of the second balcony at a symphony concert, sound travels at a nearly fixed speed, regardless of its loudness (amplitude) or its pitch (frequency). Particles, on the other hand, can easily be caused to travel at different speeds, dependent on their energy. Most important as a point of similarity, waves and particles can do the same job. Each can receive energy, carry it elsewhere, and transmit it to something else. If two girls hold the ends of a long rope, one can supply energy by shaking her end. A wave will run along the rope and transmit an impulse to the hand of the other girl. Alternatively, the same amount of energy could have been transferred by means of a “particle” such as a baseball thrown from one girl to the other.
The merging of the ideas of wave and particle was made possible only by some changes in our view of waves and of particles. Both concepts have had to yield a little in order to grow more alike. Usually we think of a wave as a vibration of something. Water waves need water, sound waves need air, the rope wave needs a rope. Before relativity made the idea untenable, it had naturally been assumed that light waves too need a material capable of vibrating: the ether. The modern idea is rather that light is the wavelike propagation of electric and magnetic fields through empty space. Quantum mechanics deals with the emission, propagation, and absorption of fields, fields associated with material particles as well as the electromagnetic field associated with photons. Because of the shift of emphasis from ether to field, we gain a new perspective on waves. A wave becomes a more material thing, an entity by itself. It is still spread out, still characterized by wavelength and frequency and amplitude, but it is something by itself, not just the name given to a vibration of an underlying medium. It is as if the girls could transmit a rope wave without a rope. This is obviously a big step in the direction of making a wave more particle-like, an unattached bundle of energy.
Quantum mechanics also brought with it some necessary changes in our view of particles, rendering them less distinct and therefore more wavelike. The most essential feature is the nonlocalizability of particles. According to the uncertainty principle, which lies at the core of quantum mechanics (Essay Q6), the location of a particle can never be precisely specified. The particle therefore loses its distinctness, becoming spread out and a bit fuzzy, like a wave. The bigger the particle, the less important is this fuzziness, so that in the world of our senses all “particles” appear to be perfectly localized and have well-defined, sharp boundaries. In the world of the very small the fuzziness becomes all-important. The fact that the hydrogen atom is 100,000 times larger than the proton at its center comes about entirely because of the nonlocalizability of the very lightweight electron, which refuses to sit quietly alongside the proton, requiring instead all of this extra space for its domain of motion (Essay Q7).
One can say that particles are nonlocalizable because they are wavelike or that they are wavelike because they are nonlocalizable. It does not really matter which one says. In practice it is somewhat simpler to take the wave nature of the particle as basic, and derive from that the other new features of quantum mechanics. The single key equation that specifies the wave nature of a particle was first postulated by Louis de Broglie in 1924; shortly afterward it was incorporated into the full theory of quantum mechanics. That the photon was in some sense both wave and particle had been known since 1905. De Broglie was the first to suggest that every particle should have a wave nature.
The de Broglie relation may be written
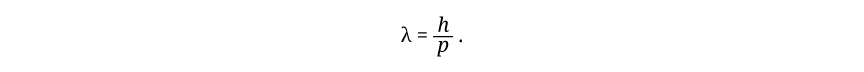This equation looks simple enough but it has consequences as significant as Einstein’s famous E = mc2. Here λ is wavelength, p is momentum, and h is Planck’s constant.
Momentum is a particle-like property. Wavelength is obviously a wavelike property. The de Broglie equation links these two properties, and the link tying them together is Planck’s constant. It is the small size of this quantum constant h that makes the wave properties of particles irrelevant except in the world of the very small. Just as with Einstein’s equation, E = mc2, where the heart of the equation is the proportionality of the energy E to the mass m, the factor c2 being a constant of proportionality, so with de Broglie’s equation, the heart of the equation is the proportionality of wavelength λ to 1/p, the inverse of the momentum p, Planck’s constant h being the constant of proportionality. Because p is in the denominator, larger p implies smaller λ. For the enormous momenta of macroscopic objects, the associated wavelength is so small that the wave property is completely unobservable. Walking at 3 miles/hr, you have a wavelength of less than 10–35 m. If you try to move more slowly in order to have a larger wavelength, it won’t help much. Progressing at one centimeter per century, your wavelength would be less than 10–23 m, still one hundred million times smaller than the size of a fundamental particle. On the other hand, a single electron moving at about 3 × 106 m/sec in the hydrogen atom has a wavelength of 2 × 10–10 m, just about the diameter of the hydrogen atom. Not until scientists extended their powers of observation far beyond the normal range of human perception did they have a chance to discover quantum mechanics.