Consider again the arrangement of Einsteins thought experiment described in Essay R6: An object at rest in the laboratory emits equal-energy photons to the left and to the right. In a moving frame of reference, the photons have neither equal energy nor equal momentum. Nevertheless, the object that emits them continues at constant speed. Since the photon momenta are unbalanced and do not add to zero, the object must suffer a change of momentum when the photons are emitted. Now if speed is constant, the only way to change momentum is to change mass. In this way, the loss of mass accompanying the photon emission can be based on momentum conservation instead of energy conservation, with the same result as before: ΔM = ΔE/c2. Here is a valuable hint, that perhaps relativity will have more to say about a connection between energy and momentum.
Another example may show even more simply the connection between momentum conservation and the mass-energy equivalence. Imagine two identical objects, each of mass m, a distance d apart. Object A emits a photon of momentum p to the right, and recoils with equal momentum p to the left. If the mass m is large and the recoil velocity v is small, the Newtonian formula for momentum, p = mv, may be used with confidence even though you have every reason to expect this formula to be incorrect at high speed. After a time t = d/c, the photon will have reached object B, and object A will have recoiled a distance x = vt = pt/m, so that at this moment objects A and B have increased their separation to the distance d + x, as shown in the figure below.
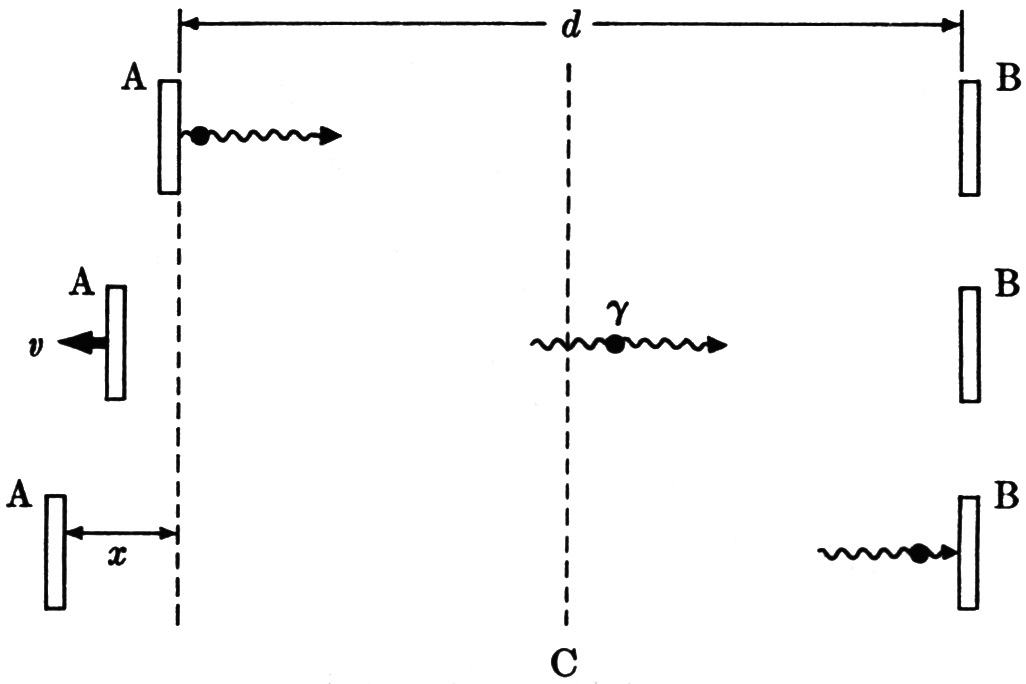Thought experiment relating momentum conservation to the mass-energy equivalence. If the center of mass of the system (indicated by the dotted line C) is to remain at rest, object A must lose some mass and object B gain some mass.
According to a general consequence of momentum conservation in classical mechanics, the center of mass of an isolated system, if once at rest, remains at rest. Yet here, apparently, the initially motionless center of mass has shifted leftward through a distance (1/2)x. To keep the center of mass riveted in place—at first halfway between the two objects, but later farther from object A than from object B—it is necessary to shift some mass. One can work out that the mass Δm lost by object A and gained by object B is equal to the photon energy divided by c2: Δm = E /c2. It seems that the photon has carried mass from A to B. This is true in a way, but the photon is nevertheless massless. It is better to say that some of the mass of object A has been transformed into the electromagnetic energy of the photon. Later this energy, upon being absorbed by B, is transformed back to mass.
Since the relativistic definition of kinetic energy implies that energy becomes infinite as the speed of a material object approaches the speed of light, it will not be surprising to learn that relativity offers a new definition of momentum with this same property. Instead of deriving the relativistic formula for momentum, which can be done in a variety of ways. I shall simply state the definition, which one can show is consistent with two other equations of relativity, the mass-energy relationship and the law of addition of velocities. Remember that momentum, like energy, is defined in such a way that it satisfies a conservation law, even at high speed, even for the interaction of matter and radiation.
Momentum is a vector quantity with the same direction as velocity and with magnitude given by
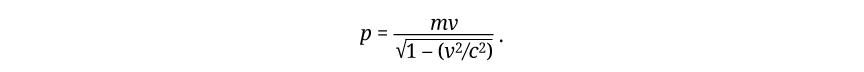The numerator is the same combination of mass and speed that defines momentum non-relativistically. The denominator is a factor that pops up frequently in the equations of relativity. Its value is imperceptibly different from one at low speed but becomes very small and produces an important effect at high speed. Since the denominator is always less than one, the relativistic momentum is always greater than the product mv: only slightly greater at low speed, but very much greater as the speed nears the speed of light. Since momentum, like kinetic energy, approached an infinite value as the speed approaches c, there is, for momentum, just as for kinetic energy, a “speed-of-light barrier” preventing motion at speeds greater than the speed of light. No matter how much momentum a particle acquires, its speed can never quite reach the limiting speed c—unless its mass is zero, an interesting special case since the massless particle can also never move more slowly than c. It is locked into a single speed.
The relativistic momentum increase was what several scientists noted in the first decade of the twentieth century when they found that high-speed electrons were more difficult to deflect than they thought they should be. This extra momentum is sometimes described by saying that a particle when moving is more massive than when stationary. But it is better not to think of the particles mass as changing, for the factor m appearing in the definition of momentum is a fixed number, regardless of how fast the particle might be moving. It is called the rest mass. The apparent mass increase comes about because a relativistic particle with fixed mass, when set in motion behaves like a Newtonian particle with increased mass. The mass increase is an illusion arising from thinking in old-fashioned Newtonian terms—namely that p = mv, a formula not valid at high speed. “Mass increase” is quite unlike, for example, time dilation, which is a real, verifiable effect of motion.