Or one could add a second neutron to the deuteron, creating a nucleus of hydrogen-3 (tritium). This is an “almost stable” nucleus, with a half life of 12.5 years. (The behavior of this nucleus [pnn] differs from that of helium-3 [ppn] because the neutron is slightly more massive than the proton.) If one added a third neutron to the deuteron, it would have to go into a higher-energy state. This would create a nucleus of hydrogen-4 (pnnn), again a very unstable nucleus, and again with a half-life of about 10–22 s.
But if one added to the deuteron not two protons or two neutrons, but instead one proton and one neutron, they would be welcomed. The resulting nucleus of helium-4 (ppnn) has all four of its nucleons in a low energy state, the two protons with oppositely directed spin, the two neutrons also with oppositely directed spin, and no restrictions on a proton and neutron occupying the same state. This is the stable nucleus of helium-4.
In summary:
| pn | stable |
| ppn or pnn | stable or almost stable |
| pppn or pnnn | very unstable |
| ppnn | stable |
The chart below, presented in the form of a graph of proton number vs. neutron number, shows nuclei that are stable (having, as far as we know, infinite half-lives) and those that are “almost stable” (having long half lives). The small squares trace out, approximately, a line, called the line of stability. At the lower left (small proton and neutron numbers), the line starts upward at a 45-degree angle reflecting the effect of the exclusion principle favoring equal or nearly equal numbers of protons and neutrons. Some nuclei in this part of the chart are helium-4 (2p-2n), carbon-12 (6p-6n), and neon-20 (10p-10n). Then the line bends over increasingly in the direction of a neutron excess—to magnesium-25 (12p-13n) and calcium-43 (20p-23n), for example; and near the upper end, uranium-238 (92p-146n). For the heaviest nuclei, the line of stability has a slope corresponding to the addition of about two neutrons for every added proton, instead of the one-to-one ratio that characterizes the light nuclei.
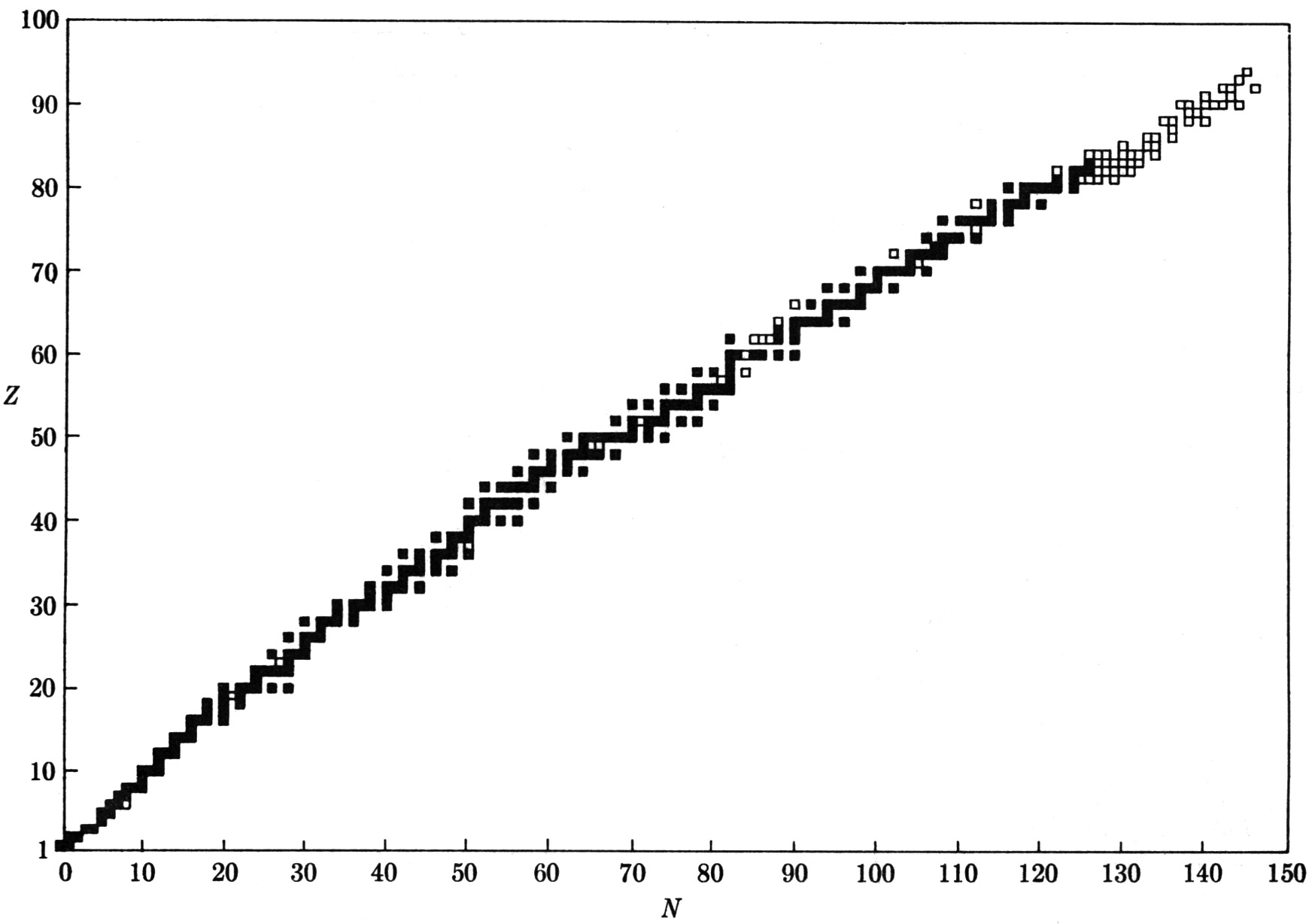
Nuclear chart. Dark squares indicate stable nuclei. Open squares indicate unstable or radioactive nuclei found in nature. Not shown are the several thousand known radioactive nuclei that have been created in the laboratory.
The line of stability not only bends. It also ends. Beyond a certain point, there are no stable nuclei, nor even any known long-lived nuclei. Both aspects of the line of stability, its shape and its termination, can be explained rather simply in terms of two effects: the action of the Pauli exclusion principle, and the action of the electrical repulsive force between protons.
At the beginning of this Essay, I discussed the role of the exclusion principle in favoring equal numbers of protons and neutrons in light nuclei. This tendency persists for heavy nuclei as well. If a proton occupies a given state of motion within the nucleus—even a heavy nucleus—an added proton must go into a different state of motion, often with greater energy. An added neutron, on the other hand, can drop into the same state of motion as the proton, since no exclusion acts between neutrons and protons. Moreover, once in identical states of motion, a neutron and a proton are in the most favorable position to experience maximum attractive force, and to contribute as much as possible to the binding energy.
Were it not for electrical forces in the nucleus, the line of stability would follow equal neutron and proton number indefinitely. Instead of about 100 known elements we might have thousands. It is the mutual electrical repulsion of protons that both bends and ends the line of stability. Only because of the great strength of the nuclear forces can protons be held together in a nucleus at all. The greater the number of protons, the greater is their tendency to blow the nucleus apart. Thus, despite the action of the exclusion principle, it becomes energetically favorable for heavy nuclei to contain more neutral particles than charged particles. Eventually, beyond 83 protons, there are no stable nuclei at all. Beyond 100 protons, there are no long-lived nuclei.
