Consider the following idealized experiment of great simplicity, which suffices to provide a basis for the definitions of work and energy. On a horizontal and ideally smooth surface, an object is pushed with a constant force FA for a time, then allowed to slide freely for a time, then decelerated and brought to rest with a constant force FC whose magnitude differs from the magnitude of the accelerating force FA. For purposes of discussion, I shall divide the motion into three parts, A, B, and C. The object begins at rest, moves in a straight line, and ends at rest. Concerning this simple motion one may ask two questions: (1) Is there any way to equate the effort required to start the object and the effort required to stop it? (2) Is there any quantity that remains constant throughout the motion? Both questions have an affirmative answer. I consider them in turn.
Comparing the accelerating phase of the motion, part A, with the decelerating phase, part C, we notice that because the magnitudes of the forces FA and FC are unequal, the distances traveled and the times elapsed are also unequal. If FC exceeds FA, the object will decelerate in less time and less distance than were required for its acceleration. However, there is one constant linking parts A and C. It is the product of force and distance in each part of the motion:
FAdA = FCdC .
This important equality can be proved using the properties of uniformly accelerated motion. Most directly it follows from a kinematic equation relating speed and distance, which, for this example, can be written
vx2 = vx02 + 2axx .
If an object has x-component of velocity vx0 at the initial point x = 0 and is accelerated in the x-direction with acceleration ax, this equation gives its x-component of velocity vx at a later point x. For our purpose we apply the equation twice, first to connect the beginning and end of part A of the motion, then to connect the beginning and end of part C of the motion. Since the speeds at the beginning of part A and at the end of part C are both zero, and since the speeds at the end of Part A and the beginning of part C are equal, a little algebraic manipulation leads to
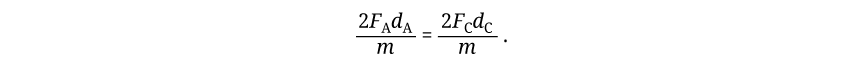 in which Newton’s second law, a = F/m, has been used.
in which Newton’s second law, a = F/m, has been used.
This, in turn, implies that the product of force and distance is, as stated above, the same in part C as in part A of the motion. The product Fd, being equal in the accelerating and decelerating parts of the motion, provides a suitable measure of the starting effort and stopping effort. Since it is independent of the particular force applied and the same for two parts of the motion, it deserves a name. It is called work, designated by W:
W = Fd .
Caution: This is a preliminary definition, valid only for a constant force applied in the direction of (or opposite to the direction of ) motion.
In this discussion I have been using the word “effort” in a loose way as a name for an overall influence that changes a state of motion. “Work,” by contrast, has a well-defined technical meaning. Before thinking about part B of the motion and how it leads to the concept of kinetic energy, it is worthwhile to examine some aspects of this new concept, work. First, it would be well to sharpen its definition. If a force acts in some direction other than the direction of motion, only the component of force parallel to the motion contributes to work. The revised definition is
W = Fǁd .
The parallel component of force needed in this definition is equal to the total magnitude of the force multiplied by the cosine of the angle between the force direction and the direction of motion. The same definition can therefore be rewritten,
W = Fd cos θ .
This revision is significant even in the example of one-dimensional motion, for if the force acts opposite to the motion instead of along the motion, the cosine is –1 instead of +1, and the work is negative instead of positive. I shall return to this point. Finally, if the force is not constant, work can be defined only over an interval so short that the change of force is negligible. The final definition of work that covers all situations is
ΔW = FǁΔs .
The increment of work, ΔW, is the product of the component of force parallel to the motion and the increment of distance moved, Δs. Despite the fact that work is defined in terms of the magnitudes of vector quantities, it is itself a scalar quantity represented by a single number. Written as a scalar product of two vectors, it is
ΔW = F• Δs.
The physical dimension of work is evidently the product of the dimensions of force and distance. Its SI unit is the newton meter (N m), or, equivalently, the kg m2/s2. This combination of units, because it is the unit of the all-important energy concept, has been given a name of its own, the joule, abbreviated J:
1 J = 1 kg m2/s2
A closely related concept worth mentioning here is power. Power is the rate of work, work per unit time (or more generally, energy per unit time). The SI power unit also has a special name, the watt, abbreviated W:
1 W = 1 J/s
The commonly encountered kilowatt is 1,000 watts.
An important fact to note about work is that it requires motion. Work is defined in terms of a change of position. Regardless of what forces may be acting on a stationary system, there is no associated work. The reason this point requires special emphasis is that the word “work” is so familiar that its many nontechnical meanings cannot lightly be abandoned in favor of a narrow new technical meaning. Actually, of course, its other meanings need not be abandoned; they need only be segregated. The physicist, in borrowing the word “work” to name a special quantitative concept, would be the last to suggest that its use in other contexts should be inhibited. She would still say that her newly repaired radio is working, that thinking is hard work, and that exerting a force through a distance on the playing field is not work, but play. It is important to avoid confusing the technical and nontechnical meanings. A boy supporting a heavy load without moving might legitimately claim to be working hard. However, if he wishes to bring the theory of mechanics to bear on his situation, he must embrace the technical definition and confess that he is doing no work.
If the work associated with a particular motion is positive, work is said to be done by the source of the force. If the work is negative, work is said to be done on the source of the force. In the example of motion considered above, work is being done by the source of the external force in part A of the motion and work is being done on the source of the external force in part C. Since the direction of the force exerted by the moving object is opposite to the direction of the force experienced by the object (Newton’s third law), the sign of the associated work is also opposite. Work is being done on the object as it accelerates and by the object as it decelerates. This means that the equality of work in part A and part C can be regarded as the manifestation of a conservation principle. Some work is expended by an outside source in part A. An exactly equal amount of work is regained by an outside source in part C. However, no work is associated with part B. Work itself is not a constant feature of the entire motion. Yet the equality of input work and output work suggests that some aspect of the motion is constant. In some way the potentiality for doing work is preserved through the intermediate region of part B. During its free motion in part B, the object possesses the ability to do work even though it is doing none.
One way to define energy in general is that which is capable of doing work. Not all forms of energy are directly or easily converted to work, but all can, through some suitable chain of transformation, manifest themselves as work. If work is done on an object (or a system), the object or system acquires an amount of energy equal to the work done (possibly, but not necessarily, in the form of kinetic energy). This relation of energy change and work can be expressed symbolically by the equation
ΔE = ΔW.
If an object does work on something else, ΔW is a negative quantity, and the object loses an amount of energy equal to the work done. The fact that we speak of energy being added to or taken away from an object does not mean that energy is regarded in any sense as an actual material substance. It can at best be called an attribute or a property of the object. Nevertheless, in order to form a mental picture of the difference between energy and work, it is helpful to think of energy as substance, work as action. A system possesses energy; it can do work. At any instant a system has a certain energy content. Part or all of this energy can be transformed into the activity of work. In one sense work is just another form of energy because of its transformability without loss to and from energy. In another sense, work is only the active measure of energy, not itself a form of energy. In still another sense (the deepest sense) there is no such thing as work at all. It is only the name for a mode of transfer of energy from one form to another. Work bears the same relation to energy that money bears to material wealth. It can be used to define and to measure energy without itself being a form of energy.
There is one other “mode of energy transfer,” and that is heat, which I address in Essay T2. Heat, like work, is often considered, incorrectly, to be a form of energy.
It is time to acknowledge the relationship of potential energy to work. Potential energy is defined only in the presence of some force, for instance the gravitational force. In fact, potential energy is nothing more nor less than a new name for the work associated with certain forces.
When a stone falls toward the ground, its gain of kinetic energy may be attributed to its loss of potential energy. Alternatively, its gain of kinetic energy may be attributed to the work done on it by the gravitational force. Either description is acceptable, but only one must be used. If the gravitational force and its associated work are taken into account explicitly, there is no need for potential energy. If potential energy is introduced, the work done by the gravitational force need not—in fact, must not—be introduced as well.
Among other forces whose effect can be represented by potential energy are the restoring force of a spring, the pull of a magnet on a nail, and the electric force between a proton and an electron. These are forces that produce recapturable energy changes. The energy expended in lifting a weight or pulling a spring or separating a nail from a magnet can be regained by lowering the weight or relaxing the spring or allowing the nail to be drawn back to the magnet. By contrast, work performed against a frictional force cannot be recaptured, at least not by simple mechanical means, for it is transformed into heat and internal energy. A frictional force is called a “dissipative” force. For it, no potential energy can be defined. For non-dissipative forces such as the force of gravity, potential energy does have meaning.
When it is possible to use potential energy in describing motion, it is usually useful to do so. For one thing, it is a scalar quantity, not a vector quantity. And, because it enters into a conservation law, it often makes easier the solution of practical problems. That is its justification. It needs no other.
