The classical laws of physics are expressed primarily as laws of change, rather than as laws of constancy. Newton’s law of motion describes how the motion of an object responds to forces that act upon it. Maxwell’s equations of electromagnetism connect the rate of change of electric and magnetic fields in space and time. The early emphasis in fundamental science was rather naturally on discovering those laws that successfully describe the changes actually occurring in nature. Briefly, the “classical” philosophy concerning nature’s laws is that scientists can imagine countless possible laws, indeed infinitely many, that might describe a particular phenomenon. Of these, nature has chosen only one simple law, and the job of science is to find it. Having successfully found laws of change, scientists may derive from them certain conservation laws, such as the conservation of energy in mechanics. These appear as particularly interesting and useful consequences of the theory, but are not themselves taken as fundamental statements of the theory.
Gradually conservation laws have percolated to the top in the hierarchy of natural laws. This importance is not merely because of their simplicity, although that has been an important factor. It comes about also for two other reasons. One is the connection between conservation laws and principles of invariance and symmetry in nature—surely, one of the most beautiful aspects of modern science. (See Essays M5 and M10). The other reason, which I wish to discuss here, might best be described simply as a new view of the world, in which conservation laws appear naturally as the most fundamental statements of natural law. This new view is a view of order upon chaos—the order of conservation laws imposed upon the chaos of continual annihilation and creation taking place in the submicroscopic world. The strong hint emerging from studies of fundamental particles is that the only inhibition imposed upon the chaotic flux of events in the world of the very small is that imposed by the conservation laws. Everything that can happen without violating a conservation law does happen.
This new view of democracy in nature—freedom under law—represents a revolutionary change in our view of natural law. The older view of a fundamental law of nature was that it must be a law of permission. It defined what can (and must) happen in natural phenomena. According to the new view, the more fundamental law is a law of prohibition. It defines what cannot happen. A conservation law is, in effect, a law of prohibition. It prohibits any phenomenon that would change the conserved quantity, but otherwise allows any events. Consider, for example, the production of pions in a proton-proton collision,
p + p → p + p + π + π + π + · · · ·
If a law of permission were operative, one might expect that, for protons colliding in a particular way, the law would specify the number and the type of pions produced. A conservation law is less restrictive. The conservation of energy limits the number of pions that can be produced, because the mass of each one uses up some of the available energy. It might say, for example, that not more than six pions can be produced. In the actual collision there might be none, or one, or any number up to six. The law of charge conservation says that the total charge of the pions must be zero, but places no restriction on the charge of any particular pion; this could be positive, negative, or neutral.
To make more clear the distinction between laws of permission and laws of prohibition, let us return to the party. A law of change, which is a law of permission, might describe the rate of arrival and the rate of departure of guests as functions of time. In simplest form, it might say that three guests per minute arrive at 6:00, two guests per minute at 6:15, and so on. Or it might say, without changing its essential character as a law of permission, that the rate of arrival of guests is given by the formula:
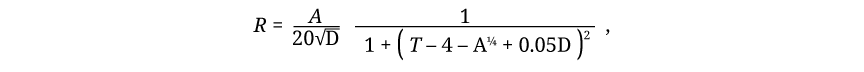where R is the number of guests arriving per minute, A is the annual income of the host in thousands of dollars, D is the distance in miles from the nearest metropolitan center (or 1 for centrally located hosts), and T is the number of hours after noon. This law resembles, in spirit, a classical law of physics. It covers many situations, but for any particular situation it predicts exactly what will happen.
A conservation law is simpler and less restrictive. Suppose it is observed that between 7 and 10 o’clock the number of guests is conserved at all parties. This is a grand general statement, appealing for its breadth of application and its simplicity. It would, were it true, be regarded as a deep truth, a very profound law of human behavior. But it gives much less detailed information than the formula for R above. The conservation law allows the guests to arrive at any rate whatever, so long as guests depart at the same rate during the specified time period. To push the analogy with natural law a bit further, we should say that according to the old view, since going to parties is a fundamental aspect of human behavior, we seek and expect to find simple explicit laws governing the flow of guests. According to the new view, we expect to find the flux of arriving and departing guests limited only by certain conservation principles. Any behavior not prohibited by the conservation laws will, sooner or later, at some party, actually occur.