An important consequence of the principle of Galilean relativity is that it is impossible to discover the existence of a truly stationary frame of reference, a frame at rest with respect to a hypothetical ether filling all of space. Since all physical phenomena (at least mechanical phenomena) follow the same laws in a frame moving uniformly with respect to this supposed ether as in a frame at rest with respect to the ether, there is no mechanical experiment that can distinguish the two. Galileo himself used the principle to support the Copernican view of the solar system. He argued that the laws of motion would be no different on a moving earth than on a stationary earth, so that one might as well adopt the simpler Copernican view of a moving earth in place of the far more complicated Ptolemaic view of a solar system built around a stationary earth. Before Galileo, almost all scientists and philosophers from Ptolemy onward had argued that the straight vertical fall of a dropped stone demonstrated that the earth must be at rest. According to Galileo’s principle of relativity, it proved no such thing.
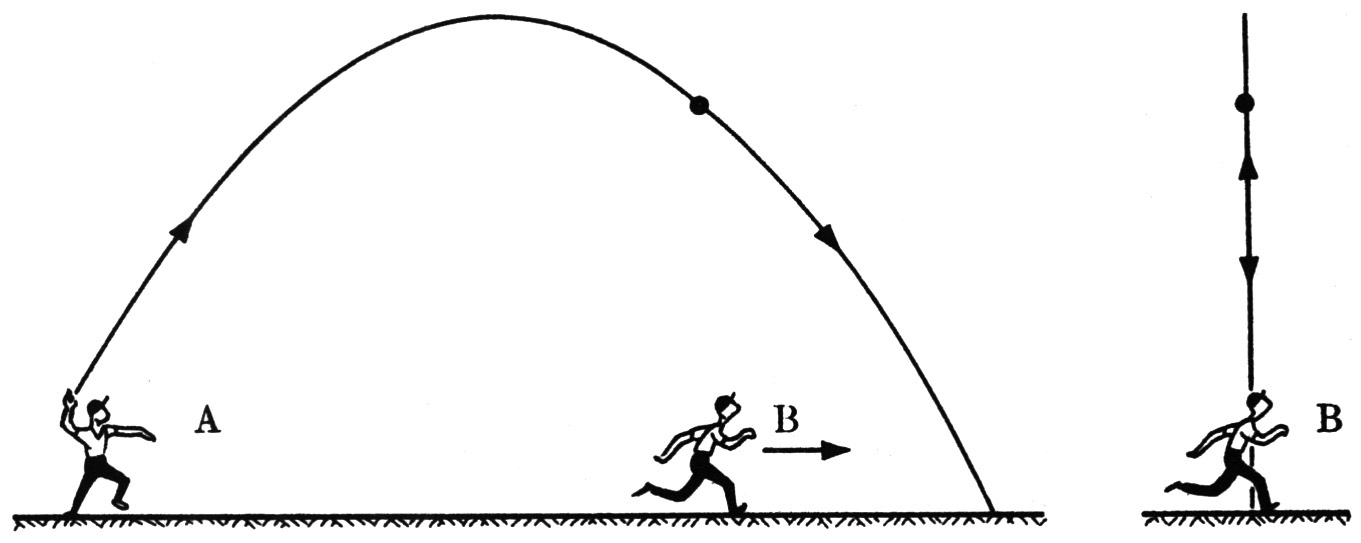
As illustrated in the figure above, two observers in relative motion disagree about the velocity of a ball whose motion they are watching. This disagreement does not prevent them from agreeing about the laws of motion because the law a = F/m does not contain velocity explicitly. It contains instead acceleration, about which the two observers agree. In the theory of electromagnetism, however, the fundamental equations do contain velocity. The magnetic field generated by a moving charge depends on the charge’s velocity. So does the magnetic force on a moving charge. And the basic equations of electromagnetism contain constants related to the speed of light. All of these velocities would be changed by a Galilean transformation. This is one reason why the laws of electromagnetism do not demonstrate Galilean invariance. They seem to call for a preferred frame of reference.
This difference between the theory of mechanics and the theory of electromagnetism can be viewed in several alternative ways.
1. The Principle of Relativity happens to be satisfied by mechanics but it is not a general principle of nature and is not very important.
2. The theory of electromagnetism is incorrect and must be changed to conform to the Principle of Relativity.
3. The Principle of Relativity is correct, but the Galilean transformation and therefore Newtonian mechanics must be discarded and a new transformation found that will permit the laws of electromagnetism to be invariant.
Einstein adopted the third bold view, which led to the theory of relativity, with its enormously successful consequences, including a new mechanics, a new view of the world, and incidentally even a deeper new insight into electromagnetism. Although the equations of electromagnetism weathered the revolution of relativity unchanged, the interpretation of these equations was somewhat altered.
Einstein’s transformation law relating the space and time measurements of different observers (all in inertial frames!) is called the Lorentz transformation. Hendrik Lorentz had shown in 1904 (a year before Einsteins “miraculous year”) that this transformation law would preserve the invariance of the theory of electromagnetism and account for the shyness of the ether. Over the course of the next five years, as scientists reluctantly but finally discarded the ether altogether, the more general validity of the Lorentz transformation and some of its startling consequences came to be realized.
The Lorentz transformation plays a vital role in the theory of relativity because it is the essential quantitative link between the measurements of different observers. Without it, science would be reduced to a chaos of subjectivity: One observer measures one thing, another measures something different, and no two observers could get together and agree about what is really happening. The Lorentz transformation is a world court of arbitration, reconciling to everyones satisfaction the divergent parochial viewpoints of scientists who insist on referring their measurements to frames of reference that are in states of relative motion. Because it accounts quantitatively for the relativity of observation, it makes possible the invariant objective agreement among different observers. Actually, human observers do not move fast enough to reveal the special features of the Lorentz transformation. However, the scientist can cast herself mathematically into a high-speed frame of reference and can describe physical processes in that frame without climbing aboard it herself.